As a teenager learning about mathematics and computers I read in a popular scientific magazine about fractals and Lorentz attractors. The beautiful fractals and my intrest in computers triggered me to develop a software that could draw fractals. On my 8088 CPU at that time the computation was awfully slow but it worked and I found it fascinating. It was a reason to me to read more about chaos theory in mathematics.
So now I decided to make a dynamic website about this intruiging mathemical phenomen. With only HTML, a canvas element, and vanilla JavaScript, it is possible to explore a mathematical object that contains infinite complexity.
This project started as an experiment in low level browser graphics and mathematical visualization. The goal was simple: render the Mandelbrot set in real time and allow interactive exploration without external libraries, frameworks, or dependencies.
What the Mandelbrot Set Really Is
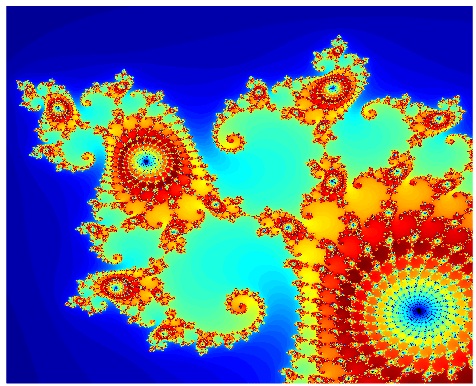
The Mandelbrot set is a collection of complex numbers for which a simple iterative formula does not diverge to infinity. The formula itself is deceptively minimal:
zₙ₊₁ = zₙ² + c
Despite its simplicity, the resulting structure reveals endless detail. No matter how deep you zoom, new patterns continue to appear. This property makes the Mandelbrot set a perfect demonstration of emergent complexity and deterministic chaos.
From a software perspective, it is also a great way to understand how numerical computation, performance, and rendering interact inside a browser.
Why Canvas and Vanilla JavaScript
This explorer is implemented using the HTML canvas API and plain JavaScript. No frameworks, no WebGL, no shortcuts.
This approach provides full control over:
• coordinate transformations
• zoom behavior
• iteration depth
• color mapping
• redraw timing
It also keeps the project readable and educational.
Interactive Exploration
The explorer supports multiple interaction modes that make the fractal feel alive.
Mouse click recenters the view and zooms in
Mouse wheel smoothly zooms in and out
Arrow keys allow precise navigation
Iteration depth increases with zoom to preserve detail
Each interaction triggers a full redraw of the canvas, recalculating every pixel based on the new parameters. While this is computationally expensive, it highlights how far modern browsers have come in raw JavaScript performance.
Coloring and Visual Feedback
Pixels that never escape the iteration limit are rendered black. All other pixels are colored using an HSL based color scheme where the hue depends on the number of iterations before escape.
A subtle hue offset animation is applied between redraws, giving the fractal a dynamic appearance without altering the underlying mathematics.
This technique makes structural boundaries more visible and enhances depth perception when zooming.
What This Project Demonstrates
Although visually appealing, this project is not about art alone. It demonstrates several core software engineering concepts.
Deterministic algorithms producing complex results
Numerical stability and floating point limitations
Performance considerations in nested loops
Event driven UI logic
State management without frameworks
It also shows that meaningful interactive software can still be built with fundamental tools, without abstraction layers.
Practical Value Beyond Visuals
Mandelbrot explorers have real world relevance beyond fascination.
They are commonly used as benchmarks for CPU and GPU performance.
They serve as teaching tools in mathematics and computer science.
They illustrate chaos theory and nonlinear systems.
They are excellent exercises for optimization and parallelization.
For developers, they are a reminder that simplicity and depth can coexist.