
DCT Discrete Cosine Transformation implementation for image processing
In digital image processing there are moments where raw pixel values are simply not the most useful representation. Pixels describe intensity at a position, but they hide structure. The Discrete Cosine Transformation, usually abbreviated as DCT, is a method that reveals structure by converting spatial information into frequency information. This idea sits at the core of JPEG image compression and many practical image processing systems.
For this project, I implemented the DCT myself in the C programming language as a proof of concept for image compression.
From pixels to frequencies
An image stored as pixels is a spatial signal. Each pixel value represents brightness at a specific location. The DCT transforms this signal into a sum of cosine waves with different frequencies and amplitudes.
Low frequency components describe slow changes in intensity such as large uniform areas or smooth gradients. High frequency components describe fast changes such as edges, sharp transitions, and noise. The important observation is that most natural images contain far more energy in the low frequencies than in the high frequencies. The DCT exploits this property very efficiently.
Why the DCT is so effective for images
The cosine basis functions used by the DCT are well matched to how intensity changes in real world images. Unlike sine based transforms, the DCT assumes even symmetry at the boundaries, which reduces discontinuities at block edges.
This has two major advantages:
First, energy compaction. A large portion of the image information ends up in a small number of coefficients.
Second, perceptual relevance. The human visual system is far more sensitive to errors in low frequencies than in high frequencies.
These properties make the DCT ideal for compression, filtering, and feature extraction.
Block based processing
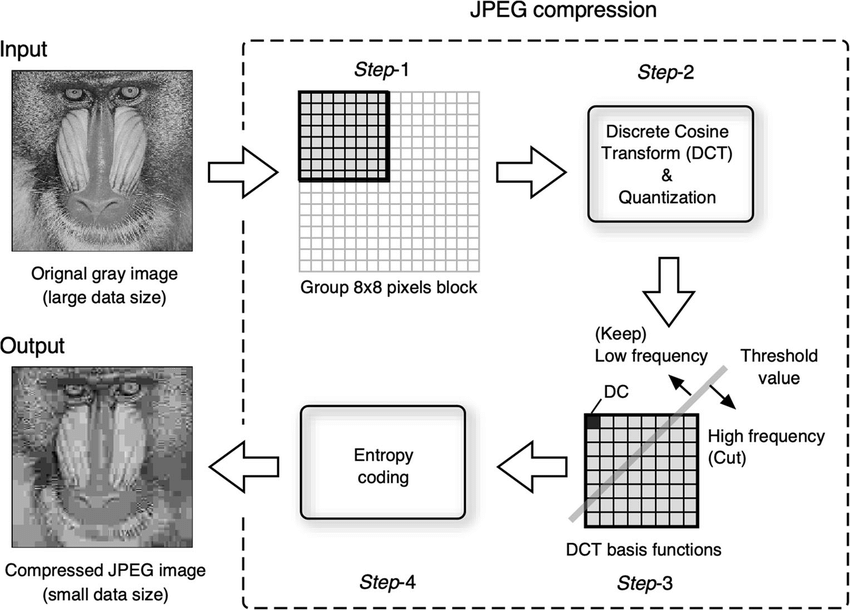
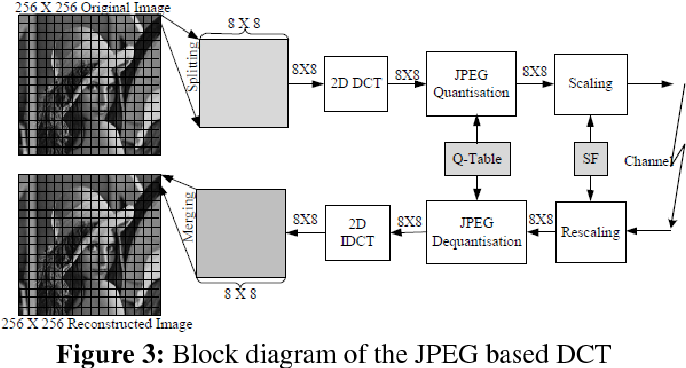
I applied the DCT to an entire image at once to show the proof of concpet. In practice the DCT is not applied to the entire image at once. Instead the image is divided into small blocks, typically 8 by 8 pixels. Each block is transformed independently. This keeps computations manageable and localizes errors. It also allows aggressive compression by discarding or coarsely quantizing high frequency coefficients within each block. This block based approach is exactly what makes JPEG efficient, but it also explains why strong compression can introduce visible blocking artifacts.
Mathematical definition
For a two dimensional block of size N by N, the DCT coefficient at position u, v is computed as a weighted sum of all pixel values in the block multiplied by cosine terms in both directions. Conceptually, each coefficient answers one question:
How much of a specific horizontal and vertical frequency is present in this block?
The coefficient at position 0,0 is the DC component. It represents the average brightness of the block. All other coefficients are AC components that describe increasing spatial frequencies.
Implementing the DCT in C
I implemented the DCT directly in C to understand every step of the transformation and to avoid black box abstractions.
The implementation follows these principles:
Nested loops for spatial to frequency conversion
Clear separation between forward DCT and inverse DCT
Removing high frequency information to achieve image compression.
Using C forces you to think about memory layout, cache behavior, and numerical stability. This is especially important in image processing where performance and determinism matter.
The core algorithm iterates over each output frequency coefficient and accumulates contributions from every input pixel in the block. Although this is computationally expensive in its naive form, it is conceptually clean and ideal for validation and learning.
Inverse DCT and reconstruction
A correct implementation must also support the inverse DCT. The inverse transformation converts frequency coefficients back into pixel values.
This step is critical to verify correctness. A forward DCT followed by an inverse DCT should reproduce the original image with only minimal numerical error.
Implementing both directions in C made it easy to insert debug checks, visualize intermediate results, and measure reconstruction error per block.
Practical applications
Beyond JPEG compression, a DCT implementation like this can be used for:
Image compression experiments
Noise reduction by suppressing high frequency coefficients
Edge detection and texture analysis
Educational tools to visualize frequency content
Because the implementation is written in C, it can be embedded easily into low level systems, real time pipelines, or custom image processing tools.
Closing thoughts
Implementing the Discrete Cosine Transformation in C is an excellent exercise in applied mathematics, numerical programming, and performance aware engineering. It forces you to understand what happens beyond libraries and APIs. The DCT is a well structured mathematical tool that, when implemented carefully, reveals why frequency domain processing is so powerful in image analysis.